wenbao与欧几里得及线性同余方程(代码片段)

扩展欧几里得：
设 a 和 b 不全为 0， 则存在整数 x 和 y ,使得
gcd(a, b) == x*a + y*b;

求解 a*x + b*y = c;   

令 d = gcd(a, b);

若 c % d == 0; 则有解　　a*x ≡ c (mod b)　　

特解可以根据扩欧求得  通解为 X = x + k*(c/d); k ~ [0,d-1]; 

令 T = b/d;

最小解为 ( X % T + T ) % T; 

以下来自博客：http://www.cnblogs.com/nwpuacmteams/articles/5545976.html

欧几里得算法的拓展应用中有如下三条定理：

   定理一：如果d = gcd(a, b)，则必能找到正的或负的整数k和l，使d = a*x+ b*y。

   定理二：若gcd(a, b) = 1，则方程ax ≡ c (mod b)在[0, b-1]上有唯一解。

   定理三：若gcd(a, b) = d，则方程ax ≡ c (mod b)在[0, b/d - 1]上有唯一解。

      证明：上述同余方程等价于ax + by = c，

如果有解，两边同除以d，就有a/d * x + b/d * y = c/d，即a/d * x ≡ c/d (mod b/d)，

显然gcd(a/d, b/d) = 1，所以由定理二知道x在[0, b/d - 1]上有唯一解。所以ax + by = c的x在[0, b/d - 1]上有唯一解，即ax ≡ c (mod b)在[0, b/d - 1]上有唯一解。

      如果得到ax ≡ c (mod b)的某一特解X，那么令r = b/gcd(a, b)，可知x在[0, r-1]上有唯一解，所以用x = (X % r + r) % r就可以求出最小非负整数解x了！

（X % r可能是负值，此时保持在[-(r-1), 0]内，正值则保持在[0, r-1]内。加上r就保持在[1, 2r - 1]内，所以再模一下r就在[0, r-1]内了）。

 推导过程：

 1 //设x、y是第一次递归的值，x1、y1是下一次递归的值，则：
 2 a*x + b*y == gcd(a, b);
 3 gcd(a, b) == gcd(b, a%b);
 4 a*x + b*y == b*x1 + a%b*y1;
 5 　　　　　　== b*x1 + (a - a/b*b)y1;
 6　　　　　　 == b*x1 + a*y1 - a/b*b*y1;
 7　　　　　　 == a*y1 + b(x1 - a/b*y1);
 8 
 9 x == y1;
10 y == x1 - a/b*y1;

 扩欧实现

 1 int x , y;
 2 int exgcd(int a, int b)
 3     if(b == 0)
 4         x = 1;
 5         y = 0;
 6         return a;
 7     
 8     int d , t;
 9     d = exgcd(b, a%b);
10     t = x;
11     x = y;
12     y = t - a/b*y;
13     return d;
14 

 小刘

1 void exgcd(int a, int b, int& d, int& x, int& y)
2     if(!b) d = a, x = 1, y = 0;
3     else exgcd(b, a%b, d, y, x), y -= x*(a/b);
4 

 大神博客：

http://www.cnblogs.com/heweiyou1993/p/3301886.html

以下均来以上博客

定义

a,b是整数，m是正整数，形如a * x ≡ b (mod m)，且x是未知数的同余式称为一元线性同余方程。

理论基础与求解

定理1:假设d = gcd(a , m)，假设对于整数xx和yy有 d = a * xx + m * yy。若d|b（d能够整出b），那么方程 a * x ≡ b (mod m)有一个解X满足式子 X = xx * (a/b) % m ，其中xx可以用扩展欧几里得算法获得。

证明1：假设上述成立那么有 a * X ≡ a * xx * (b/d)(mod m),由于a * xx ≡ d (mod m),所以可得到 a * X ≡ d * (b/d)(mod m) ≡ b(mod m)。

定理2：对于a * x ≡ b (mod m)，若有解则必有d = gcd( a, m)个解。其解为 res = (X + i * ( b / d)) (mod m)，其中X为远同余方程的一个解，i的取值范围为 0 <= i < d。

证明2：若定理2成立则有 a * res (mod m) = a * (X + i * (b / d)) (mod m) = a * X + a* i * (b /d) (mod m) = a * X (mod m) = b。

最小正整数解

由于一元线性同余方程的通解可以写成res = ( X + i * (b /d) )  (mod m) = X + i * (m/d) + m * y，由于 y 与 i 均为变量因此可以将其合并得到式子 res = X + y * ( m/d)   （其中将原式中的 m * y 看做 m/d  * d * y，由于y是变量因此可以将 d*y这个整体看为 y）,因此可以得到res = X(mod m/d) ，设m/d 为 t ，其最小正整数解可表示为 (X%t + t) % t。

@　　五指山

http://acm.nefu.edu.cn/JudgeOnline/problemShow.php?problem_id=84

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long
 4 ll x, y, d, xx, yy, M, a, b;
 5 void exgcd(ll a, ll b, ll& d, ll& x, ll& y)
 6     if(!b) d = a, x = 1, y = 0;
 7     else exgcd(b, a%b, d, y, x), y -= x*(a/b);
 8 
 9 int main()
10     int t;
11     cin >> t;
12     while(t--)
13         cin >> b >> a >> xx >> yy;
14         ll M = yy - xx;
15         exgcd(a, b, d, x, y);
16         if(M % d == 0)
17             x = x * (M/d);
18             ll w = b/d;
19             cout << (x%w + w) %w<<endl;
20         else
21             cout << "Impossible" << endl;
22         
23     
24     return 0;
25 

http://poj.org/problem?id=2115

求循环次数

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long
 4 ll x, y, d, xx, yy, M, a, b;
 5 void exgcd(ll a, ll b, ll& d, ll& x, ll& y)
 6     if(!b) d = a, x = 1, y = 0;
 7     else exgcd(b, a%b, d, y, x), y -= x*(a/b);
 8 
 9 int main()
10     while(cin >> xx >> yy >> a >> b)
11         if(xx == 0 && yy == 0 && a == 0 && b == 0) break;
12         b = 1LL << b;  //这里需要强制转化一下。。。。
13         M = yy - xx;
14         exgcd(a, b, d, x, y);
15         if(M % d == 0)
16             x = x * (M/d);
17             ll w = b/d;
18             cout << (x%w + w) %w<<endl;
19         else
20             cout << "FOREVER" << endl;
21         
22     
23     return 0;
24 

@　　http://poj.org/problem?id=2142

　　　　天平称重　　

 1 #include <iostream>
 2 #include <cmath>
 3 using namespace std;
 4 int a, b, c, d, x, y, w, M, X1, Y1, X2, Y2, mi, N;
 5 void exgcd(int a, int b, int& d, int& x, int& y)
 6     if(!b) d = a, x = 1, y = 0;
 7     else exgcd(b, a%b, d, y, x), y -= x*(a/b);
 8 
 9 int main()
10     while(cin>>a>>b>>c,a,b,c)
11         exgcd(a, b, d, x, y);
12         x = x*(c/d);
13         w = b/d;
14         X1 = (x%w + w)%w;
15         Y1 = (c-a*X1)/b;
16         if(Y1<0) Y1 = -Y1;
17         y = y*(c/d);
18         w = a/d;
19         Y2 = (y%w + w)%w;
20         X2 = (c-Y2*b)/a;
21         if(X2<0) X2 = -X2;
22         if(X1+Y1<X2+Y2) cout<<X1<< " " <<Y1 << endl;
23         else cout << X2 << " " << Y2<<endl;
24     
25     return 0;
26 

http://codeforces.com/contest/724/problem/C、

光线反射

啦啦啦啦。。。。就是这个题让我学习了拓展欧几里得。。。

 1 #include <iostream>
 2 using namespace std;
 3 #define ll long long
 4 #define INF 1e15
 5 ll n, m, k, mx, xx, yy, a, b, d, x, y, sum, M;
 6 void exgcd(ll a, ll b, ll& d, ll& x, ll& y)
 7     if(!b) d = a, x = 1, y = 0;
 8     else exgcd(b, a%b, d, y, x), y -= x*(a/b);
 9 
10 void solve(ll c, ll xx)
11     if(c%d != 0) return ;
12     sum =min(sum,((x*(c/d))%M+M)%M*n+xx);
13 
14 int main()
15     cin >> n >> m >> k, n*=2, m*=2;
16     exgcd(n, m, d, x, y), M = m/d;
17     while(k--)
18         sum = INF;
19         cin >> xx >> yy;
20         solve(yy-xx, xx), solve(m-yy-xx, xx), solve(yy-n+xx, n-xx), solve(m-yy-n+xx, n-xx);
21         cout<<(sum == INF ? -1 : sum)<<endl;
22     
23 

以下来自大神博客http://blog.csdn.net/zhjchengfeng5/article/details/7786595

扩展欧几里德算法

    谁是欧几里德？自己百度去

    先介绍什么叫做欧几里德算法

    有两个数 a b，现在，我们要求 a b 的最大公约数，怎么求？枚举他们的因子？不现实，当 a b 很大的时候，枚举显得那么的naïve ，那怎么做？

    欧几里德有个十分又用的定理： gcd(a, b) = gcd(b , a%b) ，这样，我们就可以在几乎是 log 的时间复杂度里求解出来 a 和 b 的最大公约数了，这就是欧几里德算法，用 C++ 语言描述如下：

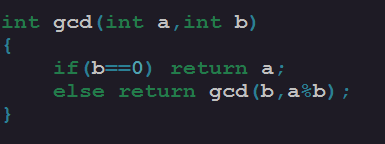
    由于是用递归写的，所以看起来很简洁，也很好记忆。那么什么是扩展欧几里德呢？

    现在我们知道了 a 和 b 的最大公约数是 gcd ，那么，我们一定能够找到这样的 x 和 y ，使得: a*x + b*y = gcd 这是一个不定方程（其实是一种丢番图方程），有多解是一定的，但是只要我们找到一组特殊的解 x0 和 y0 那么，我们就可以用 x0 和 y0 表示出整个不定方程的通解：

        x = x0 + (b/gcd)*t

        y = y0 – (a/gcd)*t

    为什么不是：

        x = x0 + b*t

        y = y0 – a*t

    这个问题也是在今天早上想通的，想通之后忍不住喷了自己一句弱逼。那是因为：

    b/gcd 是 b 的因子， a/gcd 是 a 的因子是吧？那么，由于 t的取值范围是整数，你说 (b/gcd)*t 取到的值多还是 b*t 取到的值多？同理，(a/gcd)*t 取到的值多还是 a*gcd 取到的值多？那肯定又要问了，那为什么不是更小的数，非得是 b/gcd 和a/gcd ？

    注意到：我们令 B = b/gcd ， A = a、gcd ， 那么，A 和 B 一定是互素的吧？这不就证明了 最小的系数就是 A 和 B 了吗？要是实在还有什么不明白的，看看《基础数论》（哈尔滨工业大学出版社），这本书把关于不定方程的通解讲的很清楚

    现在，我们知道了一定存在 x 和 y 使得 ： a*x + b*y = gcd ， 那么，怎么求出这个特解 x 和 y 呢？只需要在欧几里德算法的基础上加点改动就行了。

    我们观察到：欧几里德算法停止的状态是： a= gcd ， b = 0 ，那么，这是否能给我们求解 x y 提供一种思路呢？因为，这时候，只要 a = gcd 的系数是 1 ，那么只要 b 的系数是 0 或者其他值（无所谓是多少，反正任何数乘以 0 都等于 0 但是a 的系数一定要是 1），这时，我们就会有： a*1 + b*0 = gcd

    当然这是最终状态，但是我们是否可以从最终状态反推到最初的状态呢？

    假设当前我们要处理的是求出 a 和 b的最大公约数，并求出 x 和 y 使得 a*x + b*y= gcd ，而我们已经求出了下一个状态：b 和 a%b 的最大公约数，并且求出了一组x1 和y1 使得： b*x1 + (a%b)*y1 = gcd ， 那么这两个相邻的状态之间是否存在一种关系呢？

    我们知道： a%b = a - (a/b)*b（这里的 “/” 指的是整除，例如 5/2=2 , 1/3=0），那么，我们可以进一步得到：

        gcd = b*x1 + (a-(a/b)*b)*y1

            = b*x1 + a*y1 – (a/b)*b*y1

            = a*y1 + b*(x1 – a/b*y1)

    对比之前我们的状态：求一组 x 和 y 使得：a*x + b*y = gcd ，是否发现了什么？

    这里：

        x = y1

        y = x1 – a/b*y1

    以上就是扩展欧几里德算法的全部过程，依然用递归写：

    依然很简短，相比欧几里德算法，只是多加了几个语句而已。

    这就是理论部分，欧几里德算法部分我们好像只能用来求解最大公约数，但是扩展欧几里德算法就不同了，我们既可以求出最大公约数，还可以顺带求解出使得： a*x + b*y = gcd 的通解 x 和 y

    扩展欧几里德有什么用处呢？

    求解形如 a*x +b*y = c 的通解，但是一般没有谁会无聊到让你写出一串通解出来，都是让你在通解中选出一些特殊的解，比如一个数对于另一个数的乘法逆元

    什么叫乘法逆元？

    这里，我们称 x 是 a 关于 m 的乘法逆元

    这怎么求？可以等价于这样的表达式： a*x + m*y = 1

    看出什么来了吗？没错，当gcd(a , m) != 1 的时候是没有解的这也是 a*x + b*y = c 有解的充要条件： c % gcd(a , b) == 0

    接着乘法逆元讲，一般，我们能够找到无数组解满足条件，但是一般是让你求解出最小的那组解，怎么做？我们求解出来了一个特殊的解 x0 那么，我们用 x0 % m其实就得到了最小的解了。为什么？

可以这样思考：

    x 的通解不是 x0 + m*t 吗？

    那么，也就是说， a 关于 m 的逆元是一个关于 m 同余的，那么根据最小整数原理，一定存在一个最小的正整数，它是 a 关于m 的逆元，而最小的肯定是在（0 , m）之间的，而且只有一个，这就好解释了。

    可能有人注意到了，这里，我写通解的时候并不是 x0 + (m/gcd)*t ，但是想想一下就明白了，gcd = 1，所以写了跟没写是一样的，但是，由于问题的特殊性，有时候我们得到的特解 x0 是一个负数，还有的时候我们的 m 也是一个负数这怎么办？

    当 m 是负数的时候，我们取 m 的绝对值就行了，当 x0 是负数的时候，他模上 m 的结果仍然是负数（在计算机计算的结果上是这样的，虽然定义的时候不是这样的），这时候，我们仍然让 x0 对abs(m) 取模，然后结果再加上abs(m) 就行了，于是，我们不难写出下面的代码求解一个数 a 对于另一个数 m 的乘法逆元：

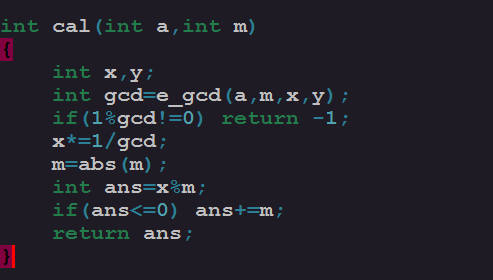
只有不断学习才能进步！